最优化理论与算法是陈宝林编写的第二版算法教程图书,由清华大学出版社出版,讲述了现行非线性、对偶原理、最优性条件等,让算法更加便捷灵活,绿色资源网欢迎大家免费下载!
最优化理论与算法pdf简介本书是陈宝林教授在多年实践基础上编著的.书中包括线性规划单纯形方法、对偶理论、灵敏度分析、运输问题、内点算法、非线性规划KKT条件、无约束最优化方法、约束最优化方法、整数规划和动态规划等内容.本书含有大量经典的和新近的算法,有比较系统的理论分析,实用性比较强;定理的证明和算法的推导主要以数学分析和线性代数为基础,比较简单易学.本书可以作为运筹学类课程的教学参考书,也可供应用数学工作者和工程技术人员参考。
最优化理论与算法电子书目录第1章引言
1.1学科简述
1.2线性与非线性规划问题
1.3几个数学概
1.4凸集和凸函数

习题
第2章线性规划的基本性质
2.1标准形式及图解法
2.2基本性质
习题
第3章单纯形方法
3.1单纯形方法原理
3.2两阶段法与大M法
3.3退化情形
3.4修正单纯形法
3.5变量有界的情形
3.6分解算法
习题
第4章对偶原理及灵敏度分析
4.1线性规划中的对偶理论
4.2对偶单纯形法
4.3原始对偶算法
4.4灵敏度分析
4.5含参数线性规划
习题
第5章运输问题
5.1运输问题的数学模型与基本性
5.2表上作业法
5.3产销不平衡运输问题
习题
第6章线性规划的内点算法
6.1Karmarkar算法
6.2内点法
6.3路径跟踪法
第7章最优性条件
7.1无约束问题的极值条件
7.2约束极值问题的最优性条件
7.3对偶及鞍点问题
习题
第8章算法
8.1算法概念
8.2算法收敛问题
习题
第9章一维搜索
9.1一维搜索概念
9.2试探法
9.3函数逼近法
习题
第10章使用导数的最优化方法
10.1最速下降法
10.2牛顿法
10.3共轭梯度法
10.4拟牛顿法
10.5信赖域方法

10.6最小二乘
习题
第11章无约束最优化的直接方法
11.1模式搜索法
11.2Rosenbrock方法
11.3单纯形搜索法
11.4Powell方法
习题
第12章可行方向法
12.1Zoutendijk可行方向法
12.2Rosen梯度投影法
12.3既约梯度法
12.4Frank?Wolfe方法
习题
第13章惩罚函数法
13.1外点罚函数法
13.2内点罚函数法
13.3乘子法
习题
第14章二次规划
14.1Lagrange方法
14.2起作用集方法
14.3Lemke方法
14.4路径跟踪法
习题
第15章整数规划简介
15.1分支定界法
15.2割平面法
15.301规划的隐数法
15.4指派问
习题
第16章动态规划简介
16.1动态规划的一些基本概念
16.2动态规划的基本定理和基本方程
16.3逆推解法和顺推解法
16.4动态规划与静态规划的关系
16.5函数迭代法
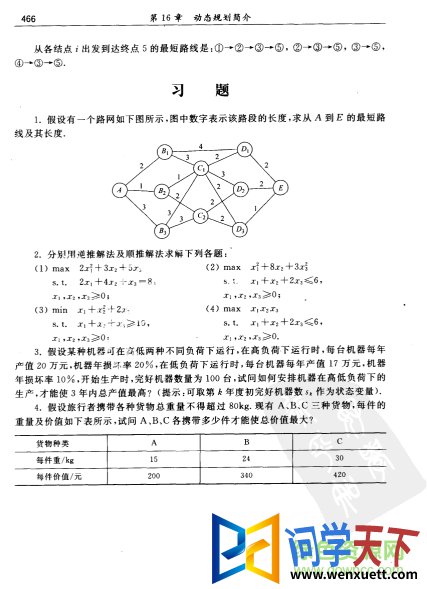
习题
参考文献
最优化理论与算法第2版内容解读本书由预备知识、线性规划、非线性规划、整数规划和动态规划五部分内容组成。在保持第1版编写风格的同时,删除了一些现在不太常用的算法,改写了部分章节,增加了含参数线性规划、运输问题、线性规划路径跟踪法、信赖域方法、二次规划路径跟踪法、整数规划、动态规划等内容。与第1版相比,第2版中的算法更加丰富,理论有所深入,在一定程度上反映出不定期些年运筹学一些分支的新进展。